Oscillatory Motion definition, examples, applications and properties

The motion of planets around the Sun is considered a periodic motion as it is repeated regularly in equal periods, The motion of spring is considered an oscillatory periodic motion, where it is a periodic motion because it is regularly repeated in equal periods and an oscillatory motion because it is repeated on the two sides of its rest position.

Types of motion

There are two types of motion, which are: Transitional motion and periodic motion. Periodic motion is a motion, which is regularly repeated in equal periods, Examples of periodic motion are Oscillatory motion and Wave motion.

Concept of oscillatory motion

Make a simple pendulum (A metallic piece, which is tied to one end of a thread, while the other end is tied to a pencil). Hold the pencil with your left hand, and pull the metallic piece (the oscillating body) to the right side, then leave it. Record the time taken by the metallic piece to repeat its movement several times.

The oscillating body moves on both sides around its rest position, This motion is repeated in equal time intervals, The displacements of the oscillating body around its rest position are equal.

The velocity of the oscillating body reaches its maximum value when it passes its rest position and decreases gradually when it goes far from it until it reaches zero at the maximum displacement on both sides of the rest position, the oscillating body moves around its rest position, where the motion is repeated through equal intervals of time which are known as “Oscillatory motion“.

Oscillatory motion is the periodic motion of the oscillating body around its real point, where the motion is repeated through equal intervals of time.

The relation between the velocity of an oscillating body and its kinetic energy (The kinetic energy = ½ (mass × squared velocity) = ½ mv².

The kinetic energy of an oscillating body is directly proportional to the mass of the oscillating body and the squared velocity of the oscillating body. So, the kinetic energy increases when the velocity of the oscillating body increases and vice versa (assuming that its mass is not changed).

The velocity of the body is taken as a measure of its kinetic energy because kinetic energy = ½ mv². The kinetic energy of a pendulum is maximum when the pendulum passes its rest position because the velocity of a pendulum is maximum when the pendulum passes its rest position and the kinetic energy is directly proportional to the square of velocity.

Application of oscillatory motion

The motion of the spring is regularly repeated in equal periods at the two sides of its rest position. The velocity of the oscillatory body (spring) is very high when it passes its resting position. The velocity of the oscillating body (spring) decreases when it goes far from its resting position until it reaches zero at the maximum displacement.

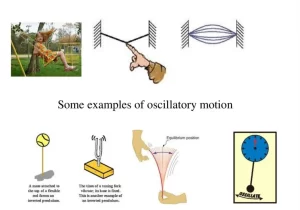
Examples of oscillatory motion:

• Tuning fork, Pendulum, Spring, Motion of swing, and Stretched string (Example: Guitar).
• The movement of Earth’s crust during earthquakes and the movement of atoms in molecules.

The motion of the rotary bee is considered as a periodic motion only because it is repeated regularly at equal time intervals, but it is not an oscillatory motion, because it is not repeated on the two sides of its rest position.

Oscillatory motion, the repetitive back-and-forth movement around a central point, is a fundamental concept in physics with widespread applications in various fields.

1. Mechanical Systems

• Clocks: Pendulum clocks utilize the consistent oscillation period of a pendulum to measure time accurately. Pendulums and quartz crystals exhibit oscillatory motion to keep accurate time.
• Shock Absorbers: Cars and motorcycles use springs and dampers to absorb vibrations through oscillatory motion, ensuring a smooth ride.
• Musical instruments: Strings, drums, and other instruments produce sound through oscillatory vibrations. Vibrating strings of musical instruments, like guitars, violins, or pianos, produce sound through oscillatory motion. 
• Bridges and buildings: Engineers consider oscillatory behavior to prevent structural failures caused by wind or earthquakes.
• Children’s Toys: Swings, seesaws, and spring-loaded toys exhibit oscillatory motion. A swing is a simple example of oscillatory motion, where the person swings back and forth around a fixed point.
• Oscillation of a Spring: Springs exhibit oscillatory motion when stretched or compressed.
• Wave Motion: Waves, whether water waves, sound waves, or light waves, exhibit oscillatory motion, carrying energy through space.

2. Electrical Systems

Electrical Circuits: Alternating current (AC) electricity oscillates, powering most of our electronic devices. The electrical power supplied to homes and industries oscillates in direction, enabling efficient power transmission. Electronic circuits generate oscillating signals used in various devices, including radios, computers, and medical equipment.

3. Nature and Science

• Atomic structure: Electrons in atoms oscillate around the nucleus, contributing to the atom’s properties. Oscillations play a vital role in atomic and subatomic systems.
• Biological systems: The human heart, lungs, and other organs undergo rhythmic oscillations.

4. Technology

• Ultrasound imaging: Medical diagnosis utilizes high-frequency sound waves to create images of internal organs.
• Magnetic resonance imaging (MRI): Powerful magnetic fields induce oscillations in hydrogen atoms, providing detailed images of the body.
• Communication systems: Radio waves, microwaves, and other forms of electromagnetic radiation involve oscillating electric and magnetic fields.

 5. Other Applications

• Seismology: The study of earthquakes involves analyzing oscillatory ground motion.
• Aerospace engineering: Aircraft wings, turbine blades, and control surfaces experience oscillatory forces during flight.
• Sports: Athletes exploit the principles of oscillation in activities like swinging a golf club or throwing a javelin.
• Manufacturing: Many industrial processes, such as cutting, drilling, and grinding, involve oscillatory tools.
• Astronomy: Celestial bodies, like planets and stars, exhibit oscillatory motion in various contexts.
• Biomedical Engineering: Heartbeats, brainwaves, and muscle contractions involve oscillatory patterns.

Simple Harmonic Motion (SHM)

• Pendulum Clocks: The swinging pendulum exhibits SHM, providing a consistent timekeeping mechanism.
• Mass-Spring Systems: Springs in cars, watches, and toys demonstrate SHM, absorbing shocks and providing energy storage.

Damped Oscillations

• Shock Absorbers: Energy is gradually dissipated to reduce the amplitude of oscillations, ensuring a smooth ride.
• Seismic Dampers: Buildings equipped with these devices reduce the impact of earthquakes by converting vibrational energy into heat.

Forced Oscillations

• Swinging a Child: Applying external force at the right frequency amplifies the swing’s motion.
• Resonance: Structures can be damaged if subjected to forces at their natural frequency (e.g., Tacoma Narrows Bridge).

Wave Motion

• Sound Waves: Oscillations of air molecules create sound, transmitted through various mediums.
• Light Waves: Electromagnetic waves, including light, exhibit oscillatory behavior.

Graphical representation of the oscillatory motion

The oscillatory motion of the spring can be represented graphically, The simple harmonic motion is considered the simplest form of oscillatory motion. In simple harmonic motion: the velocity of the oscillating body is inversely proportional to its displacement away from its rest position (A). i.e. the velocity of the oscillating body increases as it approaches the rest position (point A) and vice versa.

Properties of oscillatory motion

1. Amplitude
2. Complete oscillation
3. Periodic time
4. Frequency

Amplitude

The amplitude is the maximum displacement achieved by the oscillating body away from its rest position, The measuring unit of the amplitude is metre (m).

When the amplitude of an oscillating body is 20 cm, this means that the maximum displacement of the oscillating body away from its rest position is 20 cm

When the maximum displacement of the oscillating body is 4 cm, this means that the amplitude of the oscillating body is 4 cm (0.04m).

Complete oscillation

Complete oscillation is the motion of the oscillating body when it passes by a fixed point on its path two successive times in the same direction.

Amplitude= ¼ Complete oscillation

Distance of one complete oscillation= 4 amplitude

Periodic time

The periodic time is the time taken by the oscillating body to make one complete oscillation, the measuring unit is second (sec.). If the periodic time of an oscillating body is 0.2 sec, this means that the time taken by this oscillating body to make one complete oscillation is 0.2 sec.

Periodic time = Time in seconds/ Number of complete oscillations.

When the time taken by a spring to make 60 complete oscillations is 1 minute. this means that the periodic time of this spring is [(1× 60)/60] which equals 1 sec.

The periodic time of an oscillating body decreases as the number of complete oscillations increases at the same time because the periodic time is inversely proportional to the number of complete oscillations made by the oscillating body at a constant time.

Frequency

Frequency is the number of complete oscillations produced by an oscillation body in one second. The measuring unit is Oscillation/sec. or Hertz (Hz) Related to the German scientist Hertz. When the frequency of an oscillation body is 20 Hertz, this means that the number of complete oscillations produced by the oscillation body in one sec. is 20 complete oscillations.

Frequency= Number of complete oscillations/ Time in seconds

When the number of complete oscillations made by an oscillating body in 1 minute is 60 complete oscillations. This means that the frequency of the oscillating body is [60/ (1× 60)] which equals 1 Hz.

The value of the periodic time will be equal to that of frequency when the number of complete oscillations made by the oscillating body equals the time taken by a second.

The scientist Higenz designed the pendulum watch, considering that the pendulum oscillates at a constant frequency, whatever the amplitude changes.

Kilohertz= 1× 10³ Hertz  –   Megahertz= 1× 10⁶  Hertz   –  Gigahertz= 1× 10⁹  Hertz.

Periodic time (T) = 1/Frequency (F)

Frequency (F) = 1/Periodic time (T)

Frequency (F) × Periodic time (T) = 1

The frequency of an oscillating body is the reciprocal of the periodic time. Frequency is inversely proportional to the periodic time. the frequency decreases by increasing the periodic time and vice versa).

The frequency of the vibrating body decreases by increasing the periodic time because the frequency is inversely proportional to the periodic time.

Periodic time = Time of complete oscillation. so, Periodic time= 4 × time of amplitude.

Time of amplitude = ¼ periodic time.

You can subscribe to Science Online on YouTube from this link: Science Online  

You can download Science Online application on Google Play from this link: Science Online Apps on Google Play

Properties of Mechanical waves and Electromagnetic waves

Properties of electromagnetic waves and Light reflection

Mechanical waves and some technological applications of sound mechanical waves

Role of waves in transferring energy, Wave Motion, Transverse waves & Longitudinal waves