Ohm’s Law for closed circuit, Relation between emf (VB) of an electric cell & voltage across its poles

The emf of an electric cell (battery-source) is the total work done inside and outside the cell to transfer electric charges in the electric circuit, If we denote the emf of the battery by (V_B), the total current intensity in the circuit by (I), the external resistance by (R) and the internal resistance of the cell by (r).

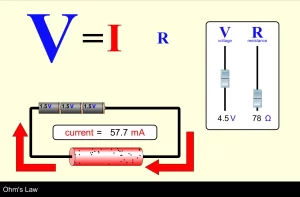
Ohm’s Law

Then: V_B = I R + I r

V_B = I (R + r)

I  =  V_B / (R + r)

This is known as Ohm’s law for a closed circuit where:

Electric current intensity = Total electromotive force / Total resistance of the circuit

The relation between emf (V_B) of an electric cell and voltage across its poles (V) 

Based on Ohm’s law for a closed circuit:

V_B = I R + I r   ,   V = I R

∴  V_B = V + I r   ,    ∴  V = V_B − I r

From the previous relation, we see that as the external resistance (R) increases, The electric current (I) passing in the circuit gradually decreases and the potential difference (V) between the poles of the cell increases.

The potential difference (V) between the poles of the cell becomes equal to the emf of the source (V_B), When the value of the current becomes very small, (I r) can be ignored.

The emf of an electric cell is greater than the potential difference between the terminal of its external circuit when the circuit is switched on, Because the internal resistance of the electric cell consumes work to pass the current inside the electric cell based on the relation (V_B = V + I r) and thus (V < V_B).

Hence we may define the emf of the cell as:

The emf of the cell (V_B) is the potential difference across poles of the cell in case of no current in the circuit (switch is opened), or it is the total work done inside and outside the cell to transfer an electric charge of 1 C (electric charges unit) in the electric circuit, The emf of the source is measured in Volt.

When the emf of an electric cell = 3 V, The total work done inside and outside the cell to transfer an electric charge of 1 C in the electric circuit = 3 J.

In the case of one electric cell connected in the circuit:

Where V_B is the reading of the voltmeter on the battery that has an internal resistance of r, the battery is connected on series with a resistance that has a potential difference of V₂ and it is connected in series with an ammeter.

If the switch K is closed:

I  =  V_B / (R + r)

I  =  V_B − V₁ / r

I  =  V₂ / R

V₂ = I  R   , V₁ = V_B − I r

If the switch K is opened:

I = 0

V₂ = 0 , V₁ = V_B

In the case of two electric cells connected in series in the circuit

Where, V₁ is the reading of the voltmeter on the first battery that has an internal resistance of r₁, V₂ is the reading of the voltmeter on the second battery that has an internal resistance of r₂,  the potential difference on the two batteries is V₃.

When the two batteries are connected in the same direction:

I  = [ ( V_B )₁ + ( V_B )₂ ] / ( R + r₁ + r₂ )

V₁ = ( V_B )₁ − I r₁

V₂ = ( V_B )₂ − I r₂

V₃ = V₁ + V₂

When the two batteries are connected in the opposite directions,  Where  (V_B)₂ < (V_B)₁:

I  = [ ( V_B )₁ − ( V_B )₂ ] / (R + r₁ + r₂)

V₁ = ( V_B )₁ − I r₁   (discharging case) 

V₂ =  ( V_B )₂ + I r₂  (charging case) 

V₃ = V₁ − V₂

Importance of Ohm’s Law for closed circuit

Ohm’s Law is a fundamental principle in electrical engineering and physics that describes the relationship between voltage, current, and resistance in a closed circuit. It is expressed as: V = I × R

Where: V is the voltage (in volts), I is the current (in amperes), and R is the resistance (in ohms).

Why Ohm’s Law is important for a closed-circuit

Ohm’s Law allows us to predict how current flows through a circuit when the voltage and resistance are known. It is essential for analyzing and designing circuits because it provides a direct relationship between these quantities.

In circuit design, Ohm’s Law helps engineers determine the proper specifications for components like resistors, capacitors, and power supplies. For instance: Choosing the right resistor value to limit current in a circuit. Ensuring components can handle the power levels determined by P = V × I

In troubleshooting closed circuits, Ohm’s Law can identify problems like:

• Open Circuits: If no current flows despite applied voltage, there might be a break in the circuit.
• Short Circuits: If resistance is near zero and current is excessively high, a short circuit may be present.

Understanding the relationship between current and resistance helps minimize energy losses. High resistance in conductors can lead to power dissipation as heat ( P = I² ×R ).

Ohm’s Law ensures safe operation by: Preventing excessive currents that could damage components or cause fires. Ensuring voltage levels are appropriate for connected devices.

Ohm’s Law is the basis for understanding more complex circuit laws and principles, such as:

• Kirchhoff’s Law is used in complex network analysis.
• Impedance in AC Circuits: Extends the concept to alternating current systems.

You can follow science online on YouTube from this link: Science online

You can download Science Online application on Google Play from this link: Science online Apps on Google Play

Properties of Electric current, Simple electric circuit, Current intensity & Potential difference

Electrical current, Potential difference, Electric resistance and Ohm’s law

Resistances connection (series & parallel), Electric energy and Electric power

Kirchhoff’s first law, Kirchhoff’s second law & how to solve problems of Kirchhoff’s laws