Gas laws, Boyle’s law and properties of gaseous materials
Particles of any material are moving in a continuous random motion, this type of motion differs according to the state of matter, So, we find that Solid molecules move in vibrational motion only, Liquid molecules move in translational and vibrational motion and Gas molecules move in random translational motion.
Properties of gaseous materials
- Gas molecules are in a continuous random motion called Brownian motion after a Scottish scientist called Brown.
- There are intermolecular spaces between gas molecules which are more or less constant for different gases.
- Gases are compressible.
Brown motion is a group of random motions of fluid particles (liquid or gas) in all directions for short distances, Brown (a Scottish scientist) discovered in 1827 that tiny pollen grains suspended in water move in a random motion.
Air (gas) molecules move in haphazard (random) motion in all directions with different velocities, During their motion they collide with each other and collide with the walls of the box, The reason for this is that the gas molecules are in a free motion and a continuous collision, so, they change their direction randomly.
Gas molecules move in random motion, During this motion, they collide with each other and collide with the walls of the container which contain them.
The compressibility of gases
If the gas is compressible, The large intermolecular spaces between molecules decrease, thus the volume occupied by the gas decreases, The volume of a gas is affected by changes in pressure as well as in temperature or both while in the case of solids or liquids, Volume changes as the temperature changes but not the pressure as they are incompressible, thus :
The experiments performed to evaluate the thermal expansion of a gas are complicated, In order to make a full study of the behavior of a gas, The relations between three variables which are the volume, pressure and temperature, which are known as (Gases laws).
Gas laws
- Boyle’s law: Study the relation between the volume and the pressure at a constant temperature.
- Charles’s law: Study the relation between the volume and the temperature at constant pressure.
- Pressure law or Jolly’s law: Study the relation between the pressure and the temperature at constant volume.
- General ( universal ) law of gases: Study the relation between pressure, volume, and temperature.
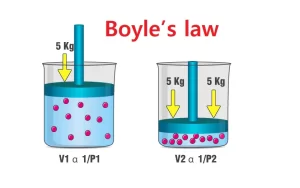
Boyle’s law
The relation between the volume and the pressure of a gas at constant temperature (Boyle’s law).
Apparatus structure: It consists of a burette (A) connected by a rubber tube to a glass reservoir (B) containing a suitable amount of mercury (A) and (B) are mounted side by side onto a vertical stand with a ruler attached to a base where the stand is adjusted vertically.
The reservoir (B) is movable along the stand either upwards or downwards and can be fixed at any desired position, The two tubes contain a suitable amount of mercury.
The following factors should be constant to verify Boyle’s law: temperature, mass of the gas, and atmospheric pressure, The burette ( A ) should be of uniform cross-sectional area so that the length of a trapped air column be a measure of a gas volume.
- Determine the atmospheric pressure (Pa) using a mercuric barometer in cm Hg.
- Open the tap (A) and move the reservoir (B) up and down until the mercury levels in the two tubes are at the same horizontal level.
- Close the tap (A) to trap a volume of air (Vol)1, Pressure P1 = Pa.
- Move reservoir (B) upwards so that the trapped air volume in reservoir (A) decreases to (Vol)2 and its pressure becomes P2 = Pa + h.
- Move reservoir (B) downwards so that the trapped air volume in reservoir (A) decreases to ( Vol )3 and its pressure becomes P3 = Pa − h.
- Repeat steps 4 , and 5 several times and each time determine P, Vol then tabulate the results.
- Draw a graphical relation between (Vol) on the (X- axis) and (1/ ρ) on the (Y- axis), So you get a straight line.
As the pressure of gas increases, the volume of the gas decreases and vice versa, So, the relation between the volume and the pressure of gas is an inverse proportionality relation.
Vol ∝ 1 / P
At constant temperature, the product of ( Vol ) and ( P ) of any given mass of gas is constant.
P Vol = Constant
Boyle’s law statement
The volume of a fixed mass of a gas is inversely proportional to the pressure, at constant temperature.
Or at constant temperature, the product of a certain volume of any given mass of a gas and its pressure is constant.
P1 / P2 = (Vol)2 / (Vol)1
Or P1 (Vol)1 = P2 (Vol)2
PV = Constant = P1 V1 = P2 V2 = P3 V3
The gas does not obey Boyle’s law in very high or very low pressures, The gas obeys Boyle’s law in the straight portion only of the graph.
If two gases are mixed with each other , we can calculate by using the following relation at constant temperature:
P Vol (mix.) = P1 (Vol)1 + P2 (Vol)2
Where: P1, and P2 represent the pressure of the two gases before mixing.
If there is an air bubble under the water surface then it is raised at the surface of the water at a constant temperature.
P1 (Vol)1 = P2 (Vol)2
(Pa + ρgh) (Vol)1 = Pa (Vol)2
Where h is the depth of the bubble inside the liquid.
If a capillary tube containing a column of mercury of length (h) trapped a certain volume of air of length (l).
When the tube is placed horizontally, then held vertically with the open end downwards.
P1 (Vol)1 = P2 (Vol)2
Pa l1 = (Pa − h) l2
When the tube is placed horizontally, then held vertically with the open end upwards.
P1 (Vol)1 = P2 (Vol)2
Pa l1 = (Pa + h) l2
Factors affecting the force of viscosity and Applications on the viscosity
Steady flow, Turbulent flow, and Applications on the continuity equation