Factors that affect work & Effect of the angle between force & displacement on work

Work

The meaning of work in physics is different from that used in everyday life , Work does not mean that a tough task is done , In physics , there are two conditions for work to be done which are the acting force and the displacement in the direction of the force .

That can be illustrated by the following two examples :

The player who lifts weights up does work because the force acting on the weights moves them upwards through a distance in the direction of the force .

The person who pushes the wall does no work because the force acting on the wall fails to move it and the wall remains motionless .

So , when a force acts on an object to move it through a certain displacement in the direction of the force , it is said that the force does work .

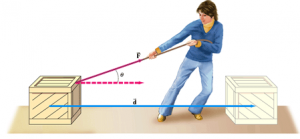
Work done ( W ) is determined by the relation :  W = F . d , Where ( F ) is the acting force and ( d ) is the displacement of the object along the line of the force action .

If the direction of the force ( F ) is inclined at an angle ( θ ) to the direction of displacement ( d ) , then ,  W = F d cos θ .

The unit of measuring work is kg.m²/s² , which is equivalent to N.m or Joule ( J ) , Dimensions of work are ML²T⁻² .

Thus work and its unit Joule are defined as follows :

Work : It is the dot product of the acting force ( F ) and the displacement ( d ) in the direction of the force .

The Joule : It is the work done by a force of one Newton to move an object through a displacement of one meter in the direction of the force .

When a person does work of 200 J on an object , It means that when this person acts on the object by a force 200 N , the object is displaced through 1 m along the line of the force action .

Although both force and displacement are vector quantities , work is a scalar quantity because work is the dot product of the force and the displacement .

Factors that affect work

The acting force on the body : Work is directly proportional to the acting force at constant displacement and constant angle between force and displacement .

Slope = W / F = d cos θ

The displacement of the body : Work is directly proportional to the displacement at constant force and constant angle between force and displacement .

Slope = W / d = F cos θ

W = F d cos θ

The angle between the force and displacement : Work is directly proportional to cosine the angle between the force and the displacement at constant force and constant displacement .

Slope = W / cos θ = F d

The effect of the angle between force and displacement on work

When the angle between the force and displacement = zero , The work done is maximum when the direction of force is the same as the direction of displacement , such as a person pulling an object through a certain distance .

W = F d cos 0° = F d

When  θ =90° , The work done is zero when the direction of force is perpendicular to the direction of displacement , W = F d cos 90° = 0 .

Example : A person moves horizontally while carrying an object where the horizontal displacement of the object is perpendicular to the direction of pulling .

When 0 ≤ θ < 90° , Work done is positive , The person does work on the object , W = F d cos θ = + ve value .

Example : A person pulling an object .

When 180° ≤ θ < 90° , Work done is negative , The object does work on the person , W = F d cos θ = − ve value .

Example : A person pulling an object while moving opposite to the direction of the force .

When  θ =180° , Work done is negative , The direction of force is opposite to the direction of displacement , W = F d cos 180 = − F d .

Example : The work done by the force of car brakes , The work done by the frictional forces .

Work done when pushing an object forwards is greater than dragging it behind , Because : On pushing , the force component ( F sin θ ) acts in the direction of the object weight ( w ) that increases friction , More work is required to move the object .

On dragging , The force component ( F sin θ ) acts opposite to the direction of the object weight ( w ) that decreases friction , Less work is required to move the object .

Finding work done graphically

Work done can be found graphically by using the ( force – displacement ) graph , If a constant force ( F ) acted on a body and displaced it through a displacement ( d ) in the direction of the force , θ = 0 .

When representing the relation ( force versus displacement ) graphically , we get a straight line parallel to displacement axis .

Work = Force × Displacement

Work ( graphically ) = Length × Width

Work = The area below the ( force – displacement ) curve .

James Joule ( 1818 – 1889 ) : An English scientist who was the first who realized that work generates heat , In one of his experiments , he found that water temperature at the bottom of a waterfall is higher than that at the top , concluding that a part of water energy is converted into heat .